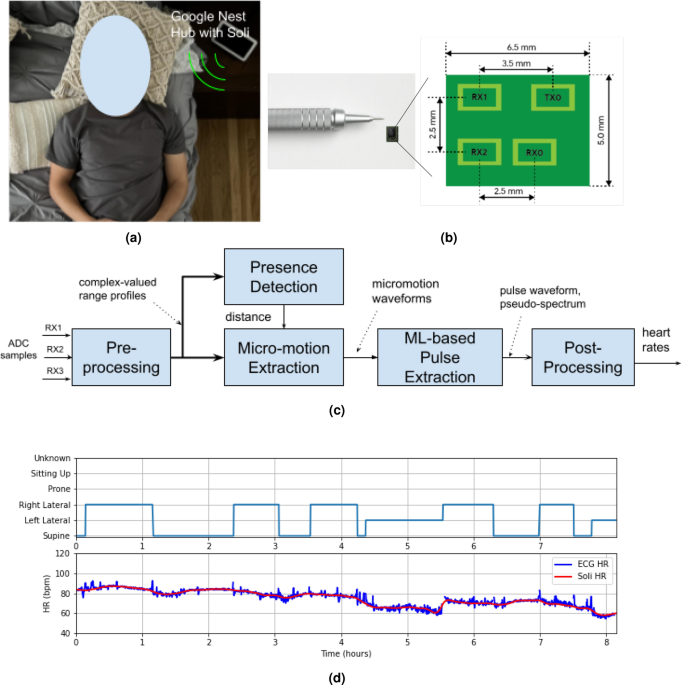
Hardware
The second-generation Soli radar chip, illustrated in Fig. 1b, is utilized in our investigation. The chip is integrated into the Google Nest Hub, as depicted in Fig. 1a. This compact chip measures \(6.5 \text{ mm } \times 5 \text{ mm } \times 0.9 \text{ mm }\) and operates at 60 GHz with one transmit antenna and three receive antennas. Its diminutive size allows for integration into various portable devices and smartphones. The receive antennas are configured in an L shape, with 2.5 mm spacing between them. The chip employs frequency-modulated continuous wave (FMCW) waveforms25, also known as chirps, with a transmit power of 5 mW. These chirps sweep frequencies from 58 GHz to 63.5 GHz, resulting in a bandwidth of \(B = 5.5\) GHz and a range resolution of approximately \(\frac{c}{2B}= 2.7\) cm, where c denotes the speed of light. The received signals are sampled at an ADC sampling rate of 2 MHz, with each chirp comprising 256 samples. Chirps are repeated at a rate of 3000 Hz, with 20 chirps organized into a burst that repeats at a burst rate of 30 Hz. The chip enters an idle mode between chirps and bursts, resulting in an active duty cycle of roughly \(\frac{256\,*\,20}{2\times 10^6} \, * \,30 = 7.68\%\) within 33 ms, compliant with the FCC wavier26. The essential operational parameters of the Soli radar chip are presented in Table 4. For a more comprehensive understanding of the Soli radar chip and the FMCW principle, interested readers may refer to the related papers16,27,28,29.
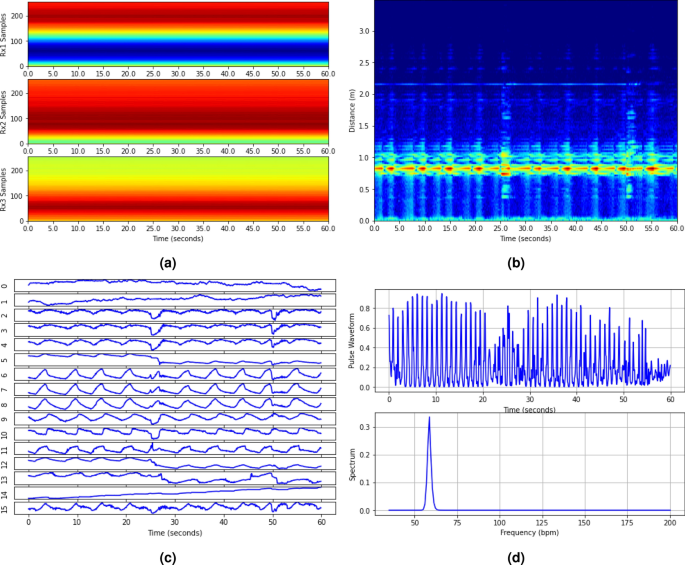
An example of noncontact HR detection for sleep tracking includes (a) ADC samples over 60 s of the three receivers, (b) combined power range profiles for presence detection, (c) extracted 16 micro-motion waveforms, and (d) pulse waveform and associated pseudo-spectrum at the NN output.
Preprocessing
The ADC samples from the three receivers are initially directed to the preprocessing block, as shown in Fig. 1c. Within the preprocessing block, the chirps within each burst are first averaged. Then the bursts are decimated from 30 to 15 Hz by merely averaging two adjacent bursts, enhancing the SNR. Consequently, the data is decimated to one chirp every 0.067 s. FFT is then applied to the decimated data along the fast-time, i.e., the 256 samples of each chirp, generating complex-valued range profiles. An example of decimated data from the three receivers of 60 s duration is illustrated in Fig. 10a, with the x-axis representing time and the y-axis representing the ADC sample index with a chirp.
Presence detection
The presence detection block in this study serves three functions: firstly, to determine whether a user is present; secondly, to determine whether the user is still; and thirdly, to determine the distance of the user from the sensor. When the presence detection block detects a still user, it will activate the subsequent HR monitoring blocks to measure the user’s HR. Conversely, it pauses the HR detection process until a still user is detected again. By including these functionalities in the presence detection block, the system can optimize HR monitoring, ensuring accurate and reliable readings are obtained.
In the presence detection stage, we first apply a clutter filter to complex-valued range profiles to eliminate strong stationary clutter originating from the background and the interplay between transmit and receive antennas. The clutter filter first calculates the average range profile over time (or chirps) and subtracts it from the original ones. It assumes that these clutter signals remain unvaried over time. The power of the so-processed range profiles is then computed and combined over receivers to form a power range profile image. As shown in Fig. 10b, the bright line in the power range profile image signifies user presence. A simple constant false alarm (CFAR)30 detector is used to detect the user and determine the associated distance. Upon user detection, the peak range bin signal is extracted from the complex-valued range profiles (after the clutter filter). An FFT is then executed to obtain a Doppler spectrum. Given that Doppler indicates the user’s motion speed, the ratio of low Doppler energy to high Doppler energy is calculated to determine the user’s stillness.
Micro-motion extraction
Once a still user is detected, 16 range bin signals are extracted from the complex-valued range profiles around the detected user distance. The micro-motion extraction algorithm is applied to each range bin independently, resulting in a micro-motion waveform.
The micro-motion extraction process involves two main steps: beamforming and phase extraction. In the first step, signals from the three receivers are combined using a maximum ratio combining (MRC) method to filter out the desired reflection signal. To perform the MRC beamforming, we first stack the signals from the three receivers into a \(3 \times 1\) vector, denoted by \(\textbf{x}(l) \in {\mathscr {C}}^{3\times 1}\), where l denotes the chirp index. A \(3 \times 3\) covariance matrix \(\textbf{Q}\) is then computed using the formula:
$$\begin{aligned}{} & {} \textbf{Q}= \frac{1}{L}\sum _{t=1}^L \left[ \textbf{x}(l) – \bar{\textbf{x}}\right] \left[ \textbf{x}(l) – \bar{\textbf{x}}\right] ^H. \end{aligned}$$
(1)
In (1), \({\hat{\textbf{x}}} = \frac{1}{L} \sum _{l=1}^L \textbf{x}(l)\) represents the stationary clutter at the current range bin, \((\cdot )^H\) denotes the Hermitian matrix transpose, and L is the number of chirps (in the example in Fig. 10, this is 900). The dominant eigenvector of \(\textbf{Q}\), denoted by \(\textbf{w}\), is computed using a power iteration method31. Finally, the three channels are combined using \(\textbf{w}\) to produce a complex-valued scalar sequence \(y(l) = \textbf{w}^H \textbf{x}(l)\).
The objective of the second step is to extract phase information from the combined signal y(l). Note that the conventional phase extraction technique is ineffective in this problem due to the small heartbeat and respiration micro-motion magnitude compared to the wavelength. Instead, a circle-fitting technique25,32 is used. This technique assumes that the desired reflection signal has a constant modulus over time. Thus, it can be formulated in the following optimization problem:
$$\begin{aligned}{} & {} \min _{\eta , r} \sum _{l} \left[ \left| y(l) – \eta \right| ^2 – r \right] ^2, \end{aligned}$$
(2)
where \(\eta \in {\mathscr {C}}\) and \(r \in {\mathscr {R}}\) represent the center and radius of the fitted circle, respectively. The optimization problem of (2) can be solved using a closed-form solution25.
Once we estimate the circle center \(\eta\), we can extract the micro-motion waveform using the following equation:
$$\begin{aligned}{} & {} d(l) = \frac{c}{4\pi f_0} \text{ unwrap }\left[ \text{ angle } (y(l) – \eta ) \right] , \end{aligned}$$
(3)
with \(f_0\) denoting the center frequency. Here, \(\text{ unwrap }(\cdot )\) denotes the unwrap function, which corrects the radian phase angles by adding multiples of \(\pm 2 \pi\) such that the phase change from the previous sample is less than \(\pi\).
Figure 10c displays the 16 micro-motion waveforms extracted from the sleep data example. While some waveforms exhibit respiration motion, the heart pulse signal is scarcely discernible. We employ an ML technique below to extract the pulse waveform and its associated pseudo-spectrum from the micro-motion waveforms.
ML-based pulse waveform and pseudo-spectrum extraction
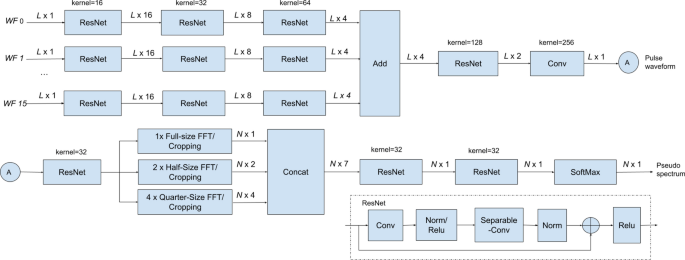
A lightweight NN for HR detection. The NN consists of two blocks. The first block extracts the pulse waveform from the 16 micro-motion waveforms, while the second block generates a pseudo-spectrum from the pulse waveform. The designed NN has 10,248 parameters, 9815 of which are trainable.
A neural network (NN) has been designed to extract the heart pulse waveform and its corresponding pseudo-spectrum from the micro-motion waveforms. The NN comprises two blocks, depicted in Fig. 11. The first block focuses on extracting the pulse waveform from the 16 micro-motion waveforms, as shown in Fig. 10c. The so-obtained pulse waveform is illustrated in the upper plot of Fig. 10d. The second block takes this pulse waveform as input and generates a pseudo-spectrum, visualized in the lower plot of Fig. 10d.
At the bottom of Fig. 11, we present a modified residual neural network (ResNet) layer33, which is utilized in both neural network (NN) blocks33. The modified ResNet layer comprises a 1D convolution (Conv) layer, followed by a separable convolution (Separable-Conv)34 layer. We use Separable-Conv for the second stage to reduce the number of parameters. A shortcut, two batch normalizations, and two rectified linear units (ReLu) are included, similar to the standard ResNet.
As shown in Fig. 11, in the first block, each of the 16 micro-motion waveforms is processed through three ResNet layers before being passed to a summation layer. The output of the summation layer is then processed through a ResNet and a standard 1D Conv layer, ultimately producing the pulse waveform output. The number of filters and their corresponding kernel size for each ResNet layer is illustrated in the figure. The ResNet weights across various input branches are enforced to be equal.
The second NN block begins by processing the pulse waveform through a ResNet layer. The resulting output is then passed through a full-size FFT layer, two half-size FFT layers, and four quarter-size FFT layers in parallel. In the half-size FFT layers, the input signal is divided into two segments, and FFT is applied to each segment independently. A similar process is used for the quarter-size FFT block. This design enhances the robustness of HR detection against random body motion, which is usually non-stationary and thus with different spectra at different time intervals. By examining the spectra at different FFT outputs, the NN can better reject the interference of random body motion. Zero-padding is applied to all 7 FFTs resulting in the same output length (1024) and the same output frequency granularity (0.88 bpm). The FFT outputs are then cropped to the frequency band of interest (35–200 bpm, \(N=189\)) and concatenated. The concatenated data is processed by two ResNet layers and one SoftMax layer, generating a pseudo-spectrum of the pulse waveform. The HR and associated confidence level can be determined by detecting the peak of the pseudo-spectrum and comparing its amplitude with that of the second peak.
The designed NN is very lightweight, with only 10,248 parameters, of which 9815 are trainable. As a result, the entire pipeline, including the NN model, data acquisition/transmission, signal processing, and virtualization, can run in real time on a laptop (e.g., MacBook Pro with 2.6 GHz 6-Core Intel Core i7) or a portable device (e.g., Google Nest Hub with Amlogic S905D3 quad-core Cortex-A55 processor), updating the HR estimate every 4 s. The NN was implemented using TensorFlow 2.13.035,36 and trained in the Google Colaboratory environment37. We used 477 h of sleep data and 478 min of meditation data for training. The training data were collected from different users using the same DC protocols as the test data. The neural network (NN) model was trained separately for sleep and meditation tracking applications due to the differences in input data lengths.
During the NN training, we utilized both the ECG and PPG waveforms, along with their respective pseudo-spectra, as ground truth labels. To facilitate ML training, we pre-processed and normalized both the ECG/PCG waveforms and their pseudo-spectra. Initially, we detected individual peaks from the raw ECG/PCG waveforms, which were then modulated by Gaussian pulses. This process effectively replaced the heartbeat pulses with standard Gaussian pulses, preserving the timing information of the heartbeats while removing other unrelated features. A similar approach was applied to process the spectrum labels. For the waveform output, a mean square error (MSE) loss function was employed, while a cross-entropy loss function was used for the pseudo-spectrum output. By combining these two loss functions, we optimized the overall performance of the NN. The Adam optimizer38 was utilized to facilitate the optimization process.
Post-processing
The HR sequence obtained from the signal processing (SP) and machine learning (ML) blocks undergoes further refinement in the post-processing block. Initially, HRs with low confidence levels are discarded, and a simple linear interpolation technique is employed to recover these rejected HR samples using neighboring samples as reference. However, if the consecutive number of rejected samples exceeds the subsequent median filter length, the HRs during that period are considered as undetermined.
A median filter is applied to ensure smoothness in the HR sequence, followed by a Gaussian smoothing filter. For sleep tracking, the median filter length is set to 10 min, while the Gaussian smoothing filter has a length of 1 min. The median and Gaussian filter lengths for meditation tracking are set to 20 s. These filter lengths are chosen to optimize the balance between preserving accurate HR information and reducing noise in the respective tracking scenarios.
Performance metrics
The accuracy of Soli HR is evaluated using five performance metrics: recall rate, MAE, MAPE, 95th percentile AE, and 95th percentile APE. The recall rate measures the percentage of data samples with determined HR values. It is calculated by dividing the number of samples with determined HRs by the total number of samples. AE and APE are computed for each determined HR sample to quantify the differences between the Soli HR and the ground-truth HR. The MAE is then determined by averaging the AEs over the investigated sample set, providing a measure of the average absolute error, i.e.,
$$\begin{aligned}{} & {} \text{ MAE } = \frac{1}{N} \sum _{n=1}^N |\text{ hr}_n – \widehat{\text{ hr }}_n|, \end{aligned}$$
(4)
with \(\text{ hr}_n\) and \(\widehat{\text{ hr }}_n\) representing the reference and estimated HRs, respectively. Similarly, the MAPE is calculated by averaging the APEs, indicating the average percentage error, i.e.,
$$\begin{aligned}{} & {} \text{ MAPE } = \frac{1}{N} \sum _{n=1}^N \frac{ \left| \text{ hr}_n – \widehat{\text{ hr }}_n \right| }{\text{ hr}_n}. \end{aligned}$$
(5)
Additionally, the 95th percentile AE and 95th percentile APE are calculated from the distribution of AEs and APEs, respectively. These metrics represent the value below which \(95\%\) of the absolute or percentage errors fall, providing insight into the performance at higher error levels.
In Tables 1 and 3, we have also included the R-squared value, denoted as \(\text{ R}^2\), as an additional metric to offer insights into the model’s performance. This statistical measure quantifies the proportion of HR variation that the model can predict compared to the total variation in HR. It is calculated as:
$$\begin{aligned}{} & {} \text{ R}^2 = 1 – \frac{ \sum _{n=1}^N \left| \text{ hr}_n – \widehat{\text{ hr }}_n \right| ^2}{ \sum _{n=1}^N \left| \text{ hr}_n – \bar{\text{ hr }} \right| ^2}, \end{aligned}$$
(6)
with \(\bar{\text{ hr }} = \frac{1}{N} \sum _{n=1}^N \text{ hr}_n\) representing the averaged HR over all data samples.
Ethical approval
All experiments and methods were performed in accordance with the relevant guidelines and regulations. Informed consent was obtained from all subjects and/or their legal guardian(s). The human heart rate collection protocol was approved by the Institutional Review Board of Google (IRB no. Pro00042166).